Types of Data & Measurement Scales: Nominal, Ordinal, Interval and Ratio
In statistics, there are four data measurement scales: nominal, ordinal, interval and ratio. These are simply ways to sub-categorize different types of data (here’s an overview of statistical data types) . This topic is usually discussed in the context of academic teaching and less often in the “real world.” If you are brushing up on this concept for a statistics test, thank a psychologist researcher named Stanley Stevens for coming up with these terms.
These four data measurement scales (nominal, ordinal, interval, and ratio) are best understood with example, as you’ll see below.
Nominal
Let’s start with the easiest one to understand. Nominal scales are used for labeling variables, without any quantitative value. “Nominal” scales could simply be called “labels.” Here are some examples, below. Notice that all of these scales are mutually exclusive (no overlap) and none of them have any numerical significance. A good way to remember all of this is that “nominal” sounds a lot like “name” and nominal scales are kind of like “names” or labels.
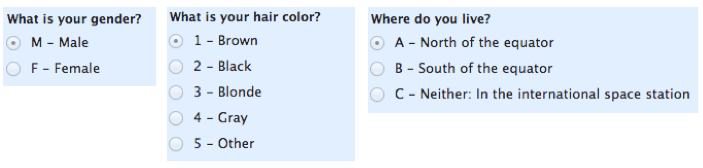
Note: a sub-type of nominal scale with only two categories (e.g. male/female) is called “dichotomous.” If you are a student, you can use that to impress your teacher.
Bonus Note #2: Other sub-types of nominal data are “nominal with order” (like “cold, warm, hot, very hot”) and nominal without order (like “male/female”).
Ordinal
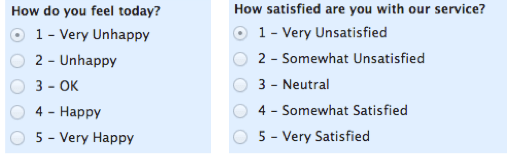
With ordinal scales, the order of the values is what’s important and significant, but the differences between each one is not really known. Take a look at the example below. In each case, we know that a #4 is better than a #3 or #2, but we don’t know–and cannot quantify–how much better it is. For example, is the difference between “OK” and “Unhappy” the same as the difference between “Very Happy” and “Happy?” We can’t say.
Ordinal scales are typically measures of non-numeric concepts like satisfaction, happiness, discomfort, etc.
“Ordinal” is easy to remember because is sounds like “order” and that’s the key to remember with “ordinal scales”–it is the order that matters, but that’s all you really get from these.
Advanced note: The best way to determine central tendency on a set of ordinal data is to use the mode or median; a purist will tell you that the mean cannot be defined from an ordinal set.
Interval
Interval scales are numeric scales in which we know both the order and the exact differences between the values. The classic example of an interval scale is Celsius temperature because the difference between each value is the same. For example, the difference between 60 and 50 degrees is a measurable 10 degrees, as is the difference between 80 and 70 degrees.
Interval scales are nice because the realm of statistical analysis on these data sets opens up. For example, central tendency can be measured by mode, median, or mean; standard deviation can also be calculated.
Like the others, you can remember the key points of an “interval scale” pretty easily. “Interval” itself means “space in between,” which is the important thing to remember–interval scales not only tell us about order, but also about the value between each item.
Here’s the problem with interval scales: they don’t have a “true zero.” For example, there is no such thing as “no temperature,” at least not with celsius. In the case of interval scales, zero doesn’t mean the absence of value, but is actually another number used on the scale, like 0 degrees celsius. Negative numbers also have meaning. Without a true zero, it is impossible to compute ratios. With interval data, we can add and subtract, but cannot multiply or divide.
Confused? Ok, consider this: 10 degrees C + 10 degrees C = 20 degrees C. No problem there. 20 degrees C is not twice as hot as 10 degrees C, however, because there is no such thing as “no temperature” when it comes to the Celsius scale. When converted to Fahrenheit, it’s clear: 10C=50F and 20C=68F, which is clearly not twice as hot. I hope that makes sense. Bottom line, interval scales are great, but we cannot calculate ratios, which brings us to our last measurement scale…

Ratio
Ratio scales are the ultimate nirvana when it comes to data measurement scales because they tell us about the order, they tell us the exact value between units, AND they also have an absolute zero–which allows for a wide range of both descriptive and inferential statistics to be applied. At the risk of repeating myself, everything above about interval data applies to ratio scales, plus ratio scales have a clear definition of zero. Good examples of ratio variables include height, weight, and duration.
Ratio scales provide a wealth of possibilities when it comes to statistical analysis. These variables can be meaningfully added, subtracted, multiplied, divided (ratios). Central tendency can be measured by mode, median, or mean; measures of dispersion, such as standard deviation and coefficient of variation can also be calculated from ratio scales.
Summary
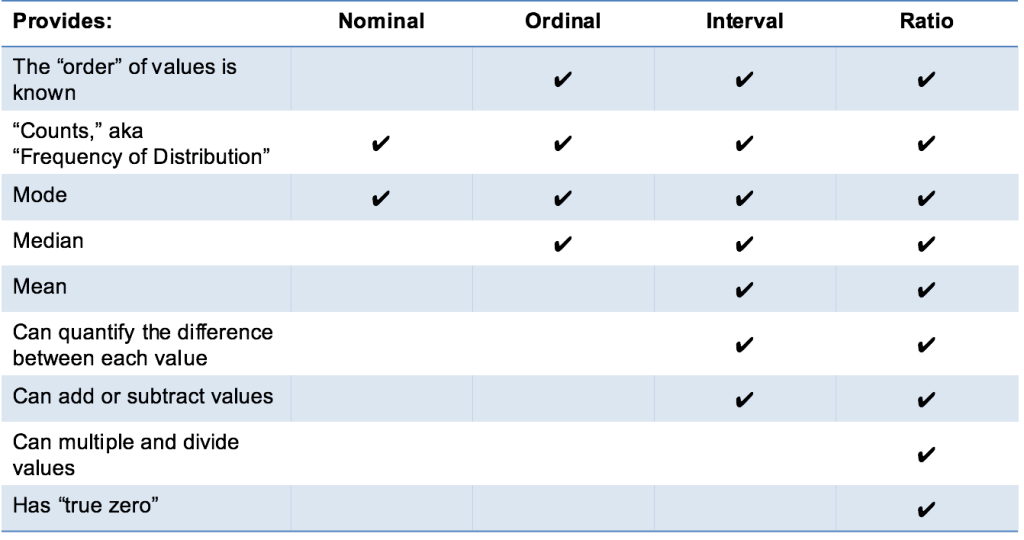
That’s it! I hope this explanation is clear and that you know understand the four types of data measurement scales: nominal, ordinal, interval, and ratio! Go get em!
If you want to test your skills, give the brief quiz below a go (not working? Try on a desktop browser):




Time is in fact a ratio scale.
20 seconds is twice as long as 10 seconds. You can multiply and divide time. The absolute 0 doesn\’t have to be attainable for the scale to be ratio. To borrow from your example: there is no such thing as \”no height\”, yet you\’ve classified height as ratio.
Thanks for the excellent comment, LJ. I have edited the article based on your comment. Perhaps the better terms are “time” and “duration,” with duration being ratio data and time being interval.
Although time does not exist on the negative scale, If its to be considered to be an interval.
I have a better understanding of the four levels of measurement. You explain the information better than my textbook.
Yes agreed, a great refresher, short sharp and concise thank you!
To avoid confusion Time and Duration are not the same.
Time is an interval measure
Duration is a ratio measure
Time is an interval measure when using any standard calendar and time measurement system as there is no fixed start point 2018/10/23:20:10 CE and 2018/10/23:20:20 CE. There is a 10 second gap but the latter is not twice the former and 2018/10/23:20:10 BCE is not effectively – (2018/10/23:20:10) CE i.e. there is no meaningful 0
Duration (the amount of time something takes) is a ratio measure as it has a meaningful zero; 20 seconds is twice as long as 10 seconds and 10 days is twice as long as 5 days.
Excellent clarification. Thank you.
Stupendous material
Thank you so much , l really understoof
But height has a definite zero. Height starts at 0.
Correct! Height is an example of a ratio scale.
Where does the cardinal lies
Please what measurement scale is blood type and birth order
blood type is nominal while birth rate could be ordinal there may interval between births but they are not on a certain scale some times could be two years and other times 5 years interval
yes, because height have true zero
Thanks for this informative text. Now I became clearer between these four terms.
Thanks for that brilliantly written info. Really helped clear all of my confusion regarding scales, especially the difference between interval and ratio. Thanks again.
Thanks this helped me a lot!
Thank you so so much. Im doing a BA in Psychotherapy and one of our modules is Psychology so we only touch on it in one class so Im not au fait at all. You have explained to me in 10 minutes what I could not understand from our lecturer in a 2 hour long lecture. Feel more confident about the exam for this module next Monday!
Thanks so much,since now i understand those scales especial to differentiate them.
Very formative article, thanks to author for such a great job!
Brilliant article though, however I had one doubt regarding oil prices in exact USD figure over a monthly period. On which scale should these values lie. Appreciate your inputs.
That would be a ratio scale. $0 is a meaningful number, and the intervals between values are equal (i.e. the difference between $1 and $2 is the same as the difference between $99 and $100). A clear indication of this fact is that you can easily multiply and divide monetary values. E.g. 1 barrel of oil costs $100, then 2 barrels will cost 2X as much, or $200.
Difficult things made really simple and easy to understand.
very helpful
Thank you very much, you are a good teacher.
much appreciated author i got informed a lot in these scales
Tnx a lot…..
THANKS. I NOW HAVE A BETTER UNDERSTANDING BETWEEN THE FOUR MEASURES
very easy to understand thank you 🙂
Thanks for the clarification
Excellent & Simple explanation with examples for clarity.
Excellent & Simple explanation.
Excellent & Simple explanation
very nice tnx
I am very impressed with your detailed and easy explanation.. wish u get reward for this 🙂
Thank you. I am very impressed with your boxing career.
This information came in handy. thank you so much.
well explained
Celsius is not really a good example for a true zero, as people experience 0 degrees Celsius quite often. A better example would be 0 degrees Kelvin. Semantics, I know, but it\’s easier to understand if phrased in K.
Great explanations otherwise.
Thank you sir. it is very helpful me for broden my knowledge.
This explanations kinda help. I wish can get more verbal explanations.
Your explanations were very explicit and illustrative. My knowledge has greatly improved on the 4 levels of measurements
I truly enjoyed reading thru this paper. Simple language, simple and to the point explanations. I appreciate you for your effort to share this with persons like me, finding hard to comprehend statistics. Thanks a lot
Thanks … It helped me a lot to understand the measurement scales.
Thanks alot
Nice work…helped me in my assingment
quiz of basic statistics
are the following nominal, ordinal, interval, or ratio data??,Explain your answers
1)Temperature measuring on a kelvin scale.
2)military ranks
3)HIV/AIDS status
4)Coli form bacteria counts in drinking water supplies
Hi Dennis,
Please find the replies in the order
1) Temperature measuring – Interval
2) military ranks – Ordinal
3) HIV/AIDS status – Nominal
4) Coli form bacteria counts in drinking water supplies – Ratio
I am doing a make up research in clinic no show rates. Taking the amount of patients scheduled on a given day, and the amount of patients that actually show. What type is this?
This article has helped me understand what I am studying, different types of vocational testing. I needed to understand the basic concept. Very helpful. Thank you
great article and very helpfull
Very precise and clear. Thank you
your explanations were simple deep,illustrative,awesome thank you keep it up
it was more informative to me and ur way of examples in each types scale was outstanding and easily to understabke thank you so much……..
give this man a bells
A very wonderful article. It really refreshed my memory. God bless you
Being a Quality Engineer. Its very important to know all the scales. This article was very informative..
Thanks
Clear and useful, thanks a lot.
Thank You. Learnt lot in a flash, summary was brilliant.
Excellent explanation for scales
Thanks alot for the detailed explanation of measurements of scale, keep it up.
That was soo simple and informative…thumbs up
I just recently signed on for a Msc in health education..and statistics is one of the modules…This is helping me a lot. Wouldnt mind more though!
Many thanks for the explanation. It helped me solve my assignment in an educational course and has also enlightened me more.
great explanation!! short and sweet, straight to the point. Awesome thanks!!
Invaluable! I found myself a gold chest. I wish I found this website so much earlier, not the day before the due like this.I will visit the website often in the future!
I think 0 is the same as 24 so we can\’t count time as ratio data even on the 24 hour clock unless you remove 24 from the data set and end at 23.
Thank you so much sir and ma\’am, this serves as my nirvana about scale of measurement. 🙂
So, Nominal & ordinal are qualitative and interval & ratio are quantitative variable. These are scale of data measurement. But ordinal can be both qualitative and quantitative. Can it?
thanks this is wonderful work.#kevin, but how would you classify the teachers job groups in a staff?
Thank you for the great job. I like the bit on how to remember, nominal is like name, ordinal is like order. That was creative. Keep it up!
Brilliant article! A very QQ: why do you classify temperature as being interval. I agree there if nothing called \\”no temperature\\” , but isn\\’t 20°c twice as hot as 10°c or am I wrong? Please clarify. Also, another ex of ratio scales would be very very helpful.
Mucho gracias, yo soy incanatado en meteriale, chao
Thanks for such clear and understandable explanation
What of binary scale?
Wow! Those examples simply nailed the explanations inside my memory. Thanks a lot.
To make things clearer, pls don’t confuse ‘true zero’ to mean that zero is a valid number on a scale.for example, the height of an individual being 0cm. ‘true zero’ means there are no negative values for the scale being considered, as in the height of a person being -100cm which is invalid. The Celsius scale is said to have ‘no true value’ because negative values are actually valid for the Celsius temperature scale. For instance , the temperature of ice could be -4 degrees Celsius. So weight and height have a true zero.
The ‘no true value’ should be ‘no true zero’ , sorry
Good clarification. thanks!
Thank you so much
Excellent!!
The clearest information ever! Thank you so much 🙂
great job.its amazing.
simplify and brief
what about these? Is the following nominal, ordinal, interval, or ratio scale?
A score of 90 out of a 100 on a test
A salary of $32.000
Ratio
thanks for such a clear explanation
You cannot multiply or divide with scores or $ eg $32 x $32, 90% / 70% – no mathematical or statistical meaning on these. Hence the example should be Interval.
Quantity of sand minned daily e.g 1-5, 6-10 trucks per day. What measurement scale is that? How can it be analyzed?
so much lucky explanation, I m 2nd year of university and I have been confused by the lecture .
but now i have got the point and impressing great thank for your helping well ,encouraging you to keep up this helping.
Brilliant explanation of an otherwise mixed up knowledge of measurement scales in some textbooks. Thanks a Lot.
Thanks very much , it help me very much I appreciate your procedure to displaying the information.
Thank you very much. Very helpful to clear my mind on measurement scales.
thanks thanks thanks.
i would also like to know in situations where interval or ordinal data is taken as nominal data.
thanks for providing such a information about better understanding of scales for measurement.
its really helpful and clear out the confusions between these scales.
provided examples really appreciable.
Yes I agree this is the best explaination I came across so far. Crystal clear and concise.
Thanks for sharing your knowledge.
BC Canada
5. Researchers at Princess Margaret Hospital measure patients’ pain using the Pain Survey where 0 = no pain and 10 = excruciating pain. What level of measurement is their survey? What measure of central tendency (mean, median, mode) can they report?
Can anyone help me with this question here, i\\’m a bit stuck
Ordinal. The best way to determine central tendency on a set of ordinal data is to use the mode or median; the mean cannot be defined from an ordinal set.
The best explanation I ever had. You are super! I wish you could be my statistic professor.
This was exactly what I needed to read. This was simple and clearly differentiated the terms quite nicely. I’m ready for my text today.
Thank you very much, I got more detail about measurment scale . I am preparing Master in Development Studies
For the question, \\\”How many courses have you taken in this year?\\\” is nominal or ratio scale?
Sounds like a ratio scale to me. Absolute zero, known order and values.
I am research scholar,i need standred scale for labour welfare measures.
Hi
I am conducting a study with four variables and in one of them, the scores are as decimals (e.g. 4.3, 5, 3.2…\”) all four variables were measured with Likert scale questionnaires, would the data still be ordinal?
Good article. On nominal/categorical data, I think you can calculate/determine the mode. Mode is the most common value in a dataset e.g. In an experiment, note what colour of shoes each participant is wearing on a particular day. Results Yellow = 5, Blue = 13 Read = 7, black = 27. Hence the mode is black since its the most occurring colour of shoes. Therefore amend the table such that you have a row for Mode, and another one for Median. Then have a tick under Ordinal, see below:
Provide Nominal Ordinal Interval Ratio
Mode Yes Yes Yes Yes
Median Yes Yes Yes
Good comment and point. I agree and will update the table. Thanks!
Great explanation
Thank you, well explained
Thank you so much!
Thanks Market Reaserch Guy
This is a very helpful article.God bless the author
thank you for the better understanding
Very well written article – concepts articulated in a simple manner. Thank You.
Thanks for this lovely article on measurement.
Great presentation and definitions. Thank you
Too good an explanation. This is by far the best article i read on scales. Crisp, candid, clear and concise. Thanks a lot.
Wow this is really good now I understand
As a physicist being forced to do pedagogical research I both appreciate this article and the image at the top. Cheers!
This is a wonderful and simple explanation – I wonder if you have considered making a video presentation and linking it to TeacherTube, Youtube, Vimeo, or some similar format? As many have already expressed, yours is perhaps one of the simplest and straightforward explanations for an otherwise complex topic.
– Just a thought
Thank you very much!
Thanks. Yes, I intend to add a video and update this post a bit once I have some time.
what is the level of measurement for bank account balance and why?
Ratio. One can have $0 balance.
Thanks for this article 🙂 u help me a lot :*
thank you so much for your help
The score of 57.11 out of 70?
What scale of measurement is used for the number of pizzas consumed during the second week/ and the number of days people got sick
Sounds like a ratio scale to me.
In which scale does nationality falls?
Nominal
Thank you.
The response has been quite helpful
Thanks is so explanatory,even with the examples.
This is really helpful and clear!, Thanks so much!
thanks, for great article.
what about Zip Code and salary
ZIP code – nominal
Salary – Ratio
Temperature is *ratio* when we use the unit Kelvin.
also want to know about difference value and absolute value. thanks
There is such a thing as no temperature. It is called absolute zero. It is represented on the Kelvin and Rankine scales, both of which have zero at absolute and are ratio data scales. The Celsius and Fahrenheit scales have zero placed arbitrarily (absolute zero exists on those scales, but is not nominally zero in either of them), and so those scales are interval but not ratio.
You have done a very good job. Please keep it up.
I am currently doing my BA in hospitality management. My research is on peoples perceptions of Self-service technology in the industry and if it is taking the hospitality element away from the experience. I am trying to work out which measurement of scale would be best used. I am using interviews to gather data.
Any help would be appreciated 🙂
Wow, what a great article. I have learnt in a few minutes what has been taught to me over the last few months (not so clearly). Really easy to read and has helped a lot. Much appreciated.
Thank you so much.
Excellent explanations with examples. Thank you so much.
I understand the definition of Interval but am having trouble applying it. Your explanation has helped some but I am still trying to wrap my brain around whether something has an absolute zero or not. What would you say the following are classified as?
Per capita income
The trade balance in dollars
Profit/loss in dollars
I have a better understanding on the four levels of measurement. You explain the meanings better than my textbook .
If the interval measure cannot be divided, then why in the chart does it say that a “mean” can be produced from it?
Very good and simple explanation
thank you !!!!!!!!!!!
thank you !
Very useful – well explained.
Thank you 🙂
Very well writeen. However, I have seek the following clarification from you.
What is your favourite sports? Answer to this will form a nominal data or ordinal data?
What kind of music do you like? It is an open ended question. Answer to this may result in more than one category like Western music, Indian music, folk music etc. How do you categorise this data? Nominal or Ordinal?
well explained… and easy to understand..
great learning for me.
nice piece of knowledge.
Simple explaination
Very useful explanation thanks a lot
Qty of mined sand daily would be ratio. 1st, there\’s a true and meaningful zero, ie, it\’s conceivable that there is a day when you get absolutely NO sand. 2nd, you can divide or multiply to get ratio of sands mined on different days, ie, 10 trucks on Monday is 2x the 5 trucks on Wed.
This is a great work ! Thanks Sir
Very very helpful article
Thank U the writer….
Excellent discussion. Very informative indeed!
Thank you, helped me with my UX studies! Greetings from Cape Town, South Africa.
Thanks for elaboration.
thank you,it helped me a lot to understand
Zero means something in interval. Just like for example in temperature there is 0°. Unlike in ratio, zero means nothing.
Great write up
Thank you for good explanation and giving clear idea about scales.
Thank you so much, your article was much better than my textbook and my teacher! Amazing!!!
Thank you! Clearer than textbooks.
Great work done by you to explain the types of measurement scales in a very simple and understandable way.thanks
Thank you so much for this explanation. You have explained it much better than my teachers and of course my textbooks.
Thank You! This was very helpful!
It helped me to understand data types in a different way.
Thanks !
Basic and precise description. It’s excellent. Thanks a lot!
I have better understanding of the explanation given
What you are talking about is time difference, which would be a ratio. Not time itself.
This makes things really simple. Thank you
Great article. I work in a business school and often use your exact temperature example, in that 20 degrees C is not twice as warm as 10 degrees. Some students can\’t visualise why though, so I\’d recommend adding a line that invites the reader to translate the same values to Fahrenheit. Once they\’ve done that conversion, everyone understands that the first statement cannot be true.
Hope this helps!
cookies and cream is indeed the best flavor.
thank you so much for this easy to understand article!!! very helpful! 🙂
Great, now I can understand these.
Very thanks.
very helpful, keep up the good work. God bless your labours
Duration is NOT interval scale. Duration is the same thing as \”time,\” which is absolutely ratio data. If John completes a task in 5 seconds and Sue completes that task in 10 seconds, we can say that John performed twice as fast.
You’re correct. I’ve updated the article. I had made a previous edit on this point, but left the sentence in the wrong section. Thanks for catching it and taking the time to point it out.
Crystal clear and precise. You have opened up my mind, continue sharing knowledge
Great article!!! I have a question… if you wanted to measure something like food consumption and the particular measurement of something in general i.e. fruit – how would you measure it using ratio scale?
Perhaps by weight.
thnak you for your effort
I’ve a couple of doubts
1. In the Nominal section you’ve mentioned like this “Nominal scales are used for labeling variables, without any quantitative value.” But in the second example, you’ve given the numerical value for classification.
2. Nominal with order is same as Ordinal ?
1 – Numbers can be used in the labeling, but the numbers don’t hold quantitative value in a nominal order.
2 – Yes, that’s a good way to put it.
I found your article very useful especially because the concepts have been explained in a simple manner with lots of examples. Many thanks.
I agree. The presentation of the concept is simple and easy to understand.
Thanks a lot. Very easy to understand.
Very informative article about data …
Interesting to learn this simple and well understood examples on scales
Thanks for your time and effort in posting.
God bless you …
Very explicit and simple. Easily understood. Thanks
I loved the way scales are explained. Very simple, especially for those who just stepping in statistics.
Well explained. Good job!
This is great!
If everything academic could be explained this way I’d ace all my Uni papers. Thanks for the explanations! I did not understand any of the scale nonsense before reading this.
T-shirt size of M, S, L & XL ill comes under which scale,
Request you to please explain
Ordinal – In this case, you know the the order of the values, but not necessarily the exact differences between each one.
Where can we classify name of student as?
Nominal
Thank you! Very clear explanation that clarified the textbook versions! Noting this would it be possible to reference (adapt) your table within a University Paper to support my choice of Ordinal Variables? (Would be greatly appreciated and referenced accordingly).
Glad you liked it. Go for it!
Thanks! Super easy to understand. Working on my doctorate and I have completely forgotten everything I learned in stats! I will be bookmarking your page!
how can you classify the ff variables?
social class
salary grade
academic ranks
your phone number
Lots of thanks; I really understood this way.
Excellent guide, many thanks for this. An example of each would’ve been great. I didn’t quite get the ‘Ratio’. Also, is there anything for a single value? For eg Like/Dislike would be Nominal (Dichotomous), however, Like only (no Dislike) would be?
Thanks
An Airline has to decide free luggage allowance and wants to study the pattern of
luggage flow
which one it will be ?
Excellent article. Simplified.
great easy to understand thanks 🙂
what type of data is T-shirt sizes
Ordinal
please would you help me answering the following questions?
1. is measure of central tendency can only be calculated in case of quantitative variables?
2.. Which measure would you use to describe the most frequent summer temperature?
A. Median
B. Mode
C. Geometric mean
3. Which statement is not true and why?
A. Not only quantitative variables have mode
B. The arithmetic mean can be calculated from any variables. Why?
C. The median can always be determined from quantitative variables. Why?
4. is the arithmetic mean always describes the distribution of data well?
very informative.
If i want to know the rank of an army officer, what would be the scale here, ordinal?
Simple and concise explanation. However, when yo have a coded response of (Yes/No) to a question like “Did this activity (weeding) take place”…will the response collected be considered as a nominal data.
and also, how will you categorize the number of times the weeding was done.
“cold, warm, hot, very hot” is a nominal scale or ordinal. Please Explain
Ordinal…you know the order of these items, but not necessary the value between each.
Great, well explained article, thank you.
How about the number of home visit ,what is the measurement?
Thanks.